Insertion sort is a sorting algorithm that places an unsorted element at its suitable place in each iteration.
Insertion sort works similarly as we sort cards in our hand in a card game.
We assume that the first card is already sorted then, we select an unsorted card. If the unsorted card is greater than the card in hand, it is placed on the right otherwise, to the left. In the same way, other unsorted cards are taken and put in their right place.
A similar approach is used by insertion sort.
Working of Insertion Sort
Suppose we need to sort the following array.

- The first element in the array is assumed to be sorted. Take the second element and store it separately in
key.
Comparekeywith the first element. If the first element is greater thankey, then key is placed in front of the first element.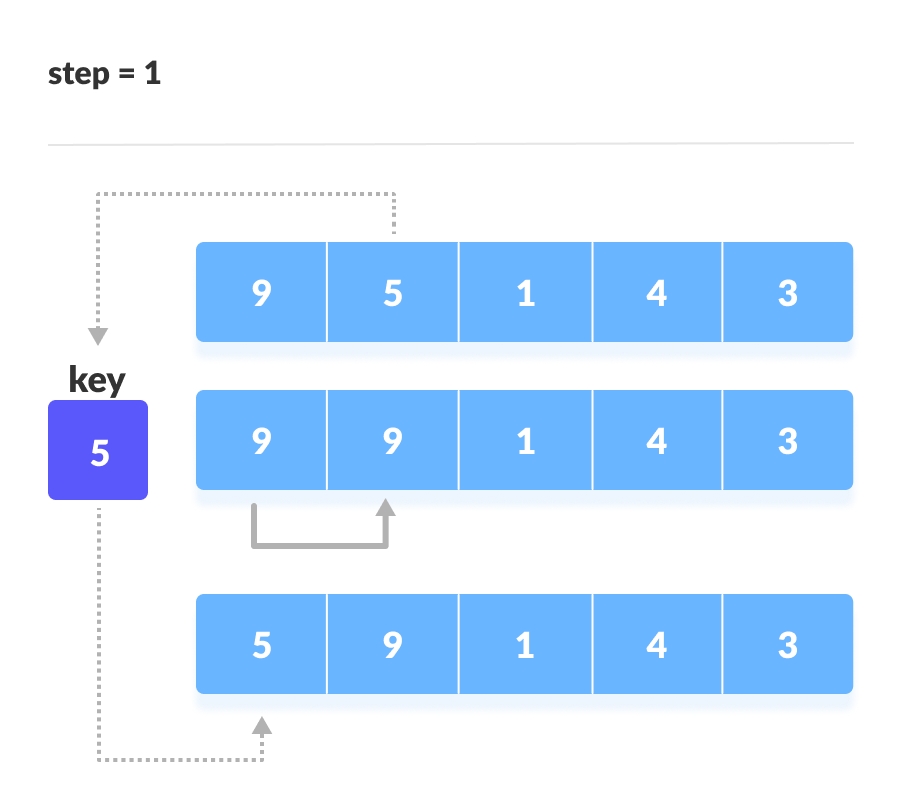
If the first element is greater than key, then key is placed in front of the first element. - Now, the first two elements are sorted.
Take the third element and compare it with the elements on the left of it. Placed it just behind the element smaller than it. If there is no element smaller than it, then place it at the beginning of the array.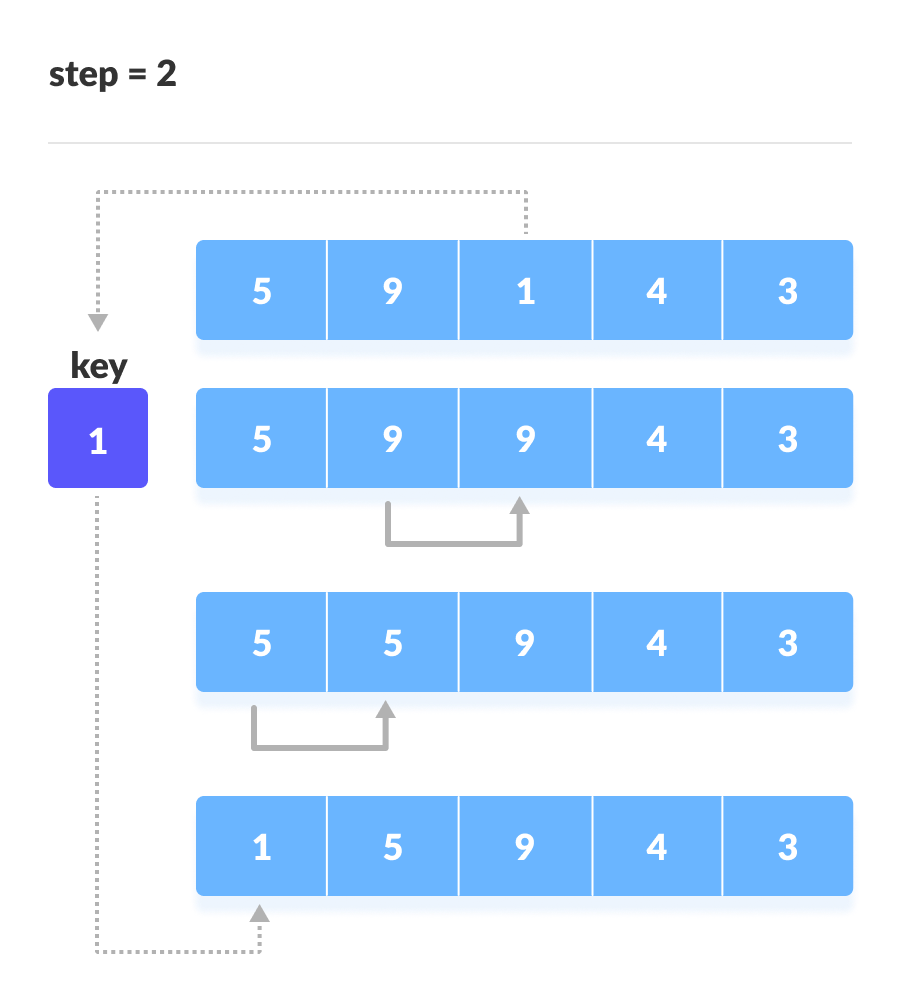
Place 1 at the beginning - Similarly, place every unsorted element at its correct position.
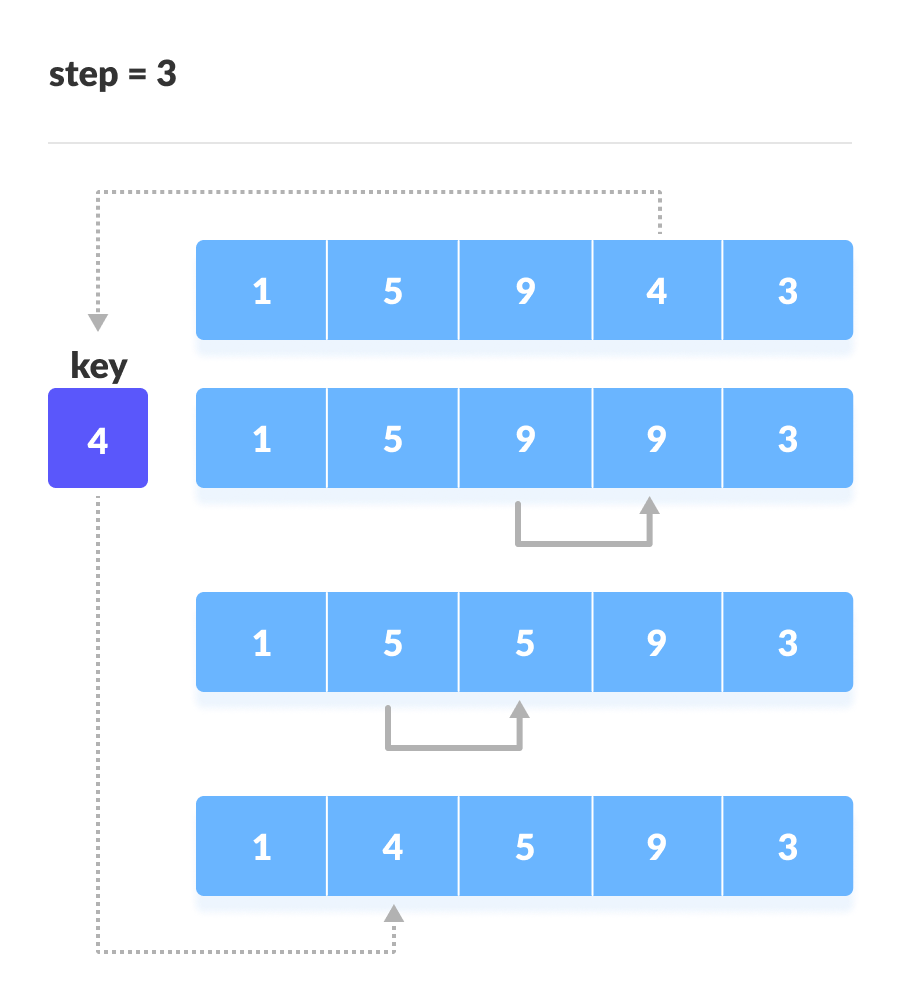
Place 4 behind 1 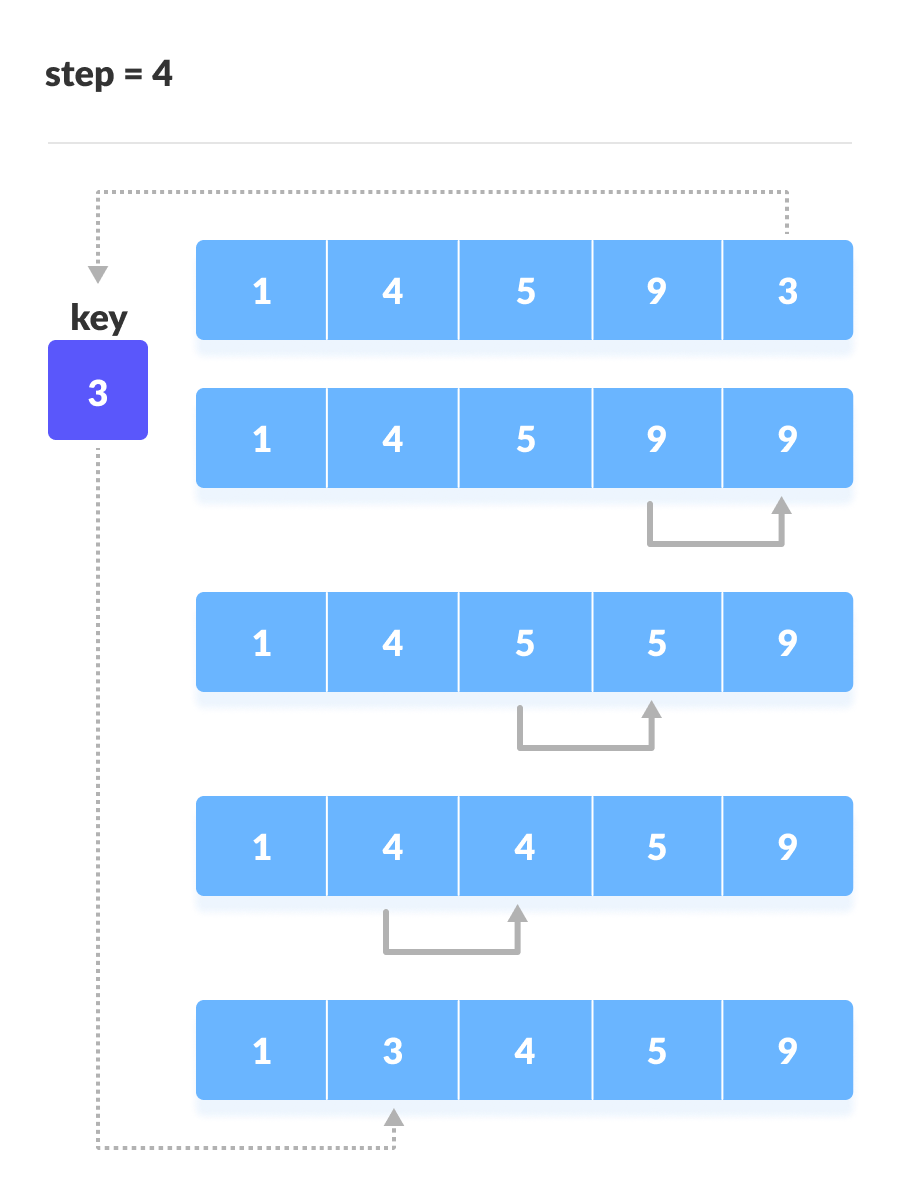
Place 3 behind 1 and the array is sorted
Insertion Sort Algorithm
insertionSort(array)
mark first element as sorted
for each unsorted element X
'extract' the element X
for j <- lastSortedIndex down to 0
if current element j > X
move sorted element to the right by 1
break loop and insert X here
end insertionSort
Insertion Sort in Python, Java, and C/C++
# Insertion sort in Python
def insertionSort(array):
for step in range(1, len(array)):
key = array[step]
j = step - 1
# Compare key with each element on the left of it until an element smaller than it is found
# For descending order, change key<array[j] to key>array[j].
while j >= 0 and key < array[j]:
array[j + 1] = array[j]
j = j - 1
# Place key at after the element just smaller than it.
array[j + 1] = key
data = [9, 5, 1, 4, 3]
insertionSort(data)
print('Sorted Array in Ascending Order:')
print(data)
// Insertion sort in Java
import java.util.Arrays;
class InsertionSort {
void insertionSort(int array[]) {
int size = array.length;
for (int step = 1; step < size; step++) {
int key = array[step];
int j = step - 1;
// Compare key with each element on the left of it until an element smaller than
// it is found.
// For descending order, change key<array[j] to key>array[j].
while (j >= 0 && key < array[j]) {
array[j + 1] = array[j];
--j;
}
// Place key at after the element just smaller than it.
array[j + 1] = key;
}
}
// Driver code
public static void main(String args[]) {
int[] data = { 9, 5, 1, 4, 3 };
InsertionSort is = new InsertionSort();
is.insertionSort(data);
System.out.println("Sorted Array in Ascending Order: ");
System.out.println(Arrays.toString(data));
}
}
// Insertion sort in C
#include <stdio.h>
// Function to print an array
void printArray(int array[], int size) {
for (int i = 0; i < size; i++) {
printf("%d ", array[i]);
}
printf("\n");
}
void insertionSort(int array[], int size) {
for (int step = 1; step < size; step++) {
int key = array[step];
int j = step - 1;
// Compare key with each element on the left of it until an element smaller than
// it is found.
// For descending order, change key<array[j] to key>array[j].
while (key < array[j] && j >= 0) {
array[j + 1] = array[j];
--j;
}
array[j + 1] = key;
}
}
// Driver code
int main() {
int data[] = {9, 5, 1, 4, 3};
int size = sizeof(data) / sizeof(data[0]);
insertionSort(data, size);
printf("Sorted array in ascending order:\n");
printArray(data, size);
}
// Insertion sort in C++
#include <iostream>
using namespace std;
// Function to print an array
void printArray(int array[], int size) {
for (int i = 0; i < size; i++) {
cout << array[i] << " ";
}
cout << endl;
}
void insertionSort(int array[], int size) {
for (int step = 1; step < size; step++) {
int key = array[step];
int j = step - 1;
// Compare key with each element on the left of it until an element smaller than
// it is found.
// For descending order, change key<array[j] to key>array[j].
while (key < array[j] && j >= 0) {
array[j + 1] = array[j];
--j;
}
array[j + 1] = key;
}
}
// Driver code
int main() {
int data[] = {9, 5, 1, 4, 3};
int size = sizeof(data) / sizeof(data[0]);
insertionSort(data, size);
cout << "Sorted array in ascending order:\n";
printArray(data, size);
}
Insertion Sort Complexity
| Time Complexity | |
|---|---|
| Best | O(n) |
| Worst | O(n2) |
| Average | O(n2) |
| Space Complexity | O(1) |
| Stability | Yes |
Time Complexities
- Worst Case Complexity:
O(n2)
Suppose, an array is in ascending order, and you want to sort it in descending order. In this case, worst case complexity occurs.
Each element has to be compared with each of the other elements so, for every nth element,(n-1)number of comparisons are made.
Thus, the total number of comparisons =n*(n-1) ~ n2 - Best Case Complexity:
O(n)
When the array is already sorted, the outer loop runs fornnumber of times whereas the inner loop does not run at all. So, there are onlynnumber of comparisons. Thus, complexity is linear. - Average Case Complexity:
O(n2)
It occurs when the elements of an array are in jumbled order (neither ascending nor descending).
Space Complexity
Space complexity is O(1) because an extra variable key is used.
Insertion Sort Applications
The insertion sort is used when:
- the array is has a small number of elements
- there are only a few elements left to be sorted