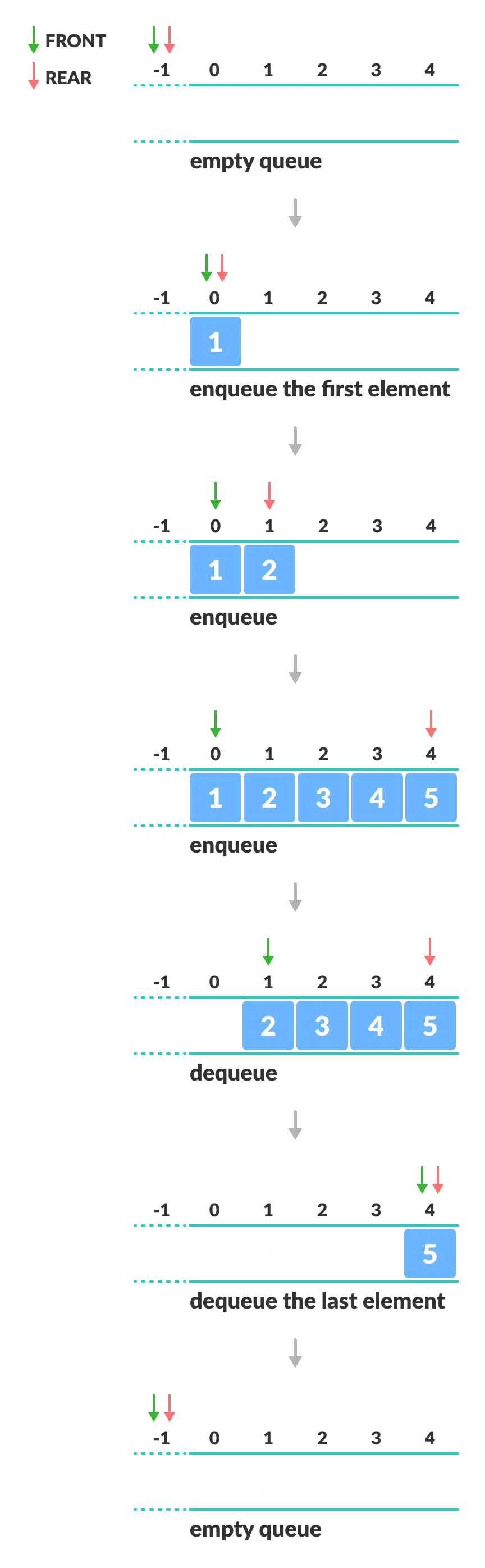
A queue is a useful data structure in programming. It is similar to the ticket queue outside a cinema hall, where the first person entering the queue is the first person who gets the ticket.
Queue follows the First In First Out (FIFO) rule - the item that goes in first is the item that comes out first.

In the above image, since 1 was kept in the queue before 2, it is the first to be removed from the queue as well. It follows the FIFO rule.
In programming terms, putting items in the queue is called enqueue, and removing items from the queue is called dequeue.
We can implement the queue in any programming language like C, C++, Java, Python or C#, but the specification is pretty much the same.
Basic Operations of Queue
A queue is an object (an abstract data structure - ADT) that allows the following operations:
- Enqueue: Add an element to the end of the queue
- Dequeue: Remove an element from the front of the queue
- IsEmpty: Check if the queue is empty
- IsFull: Check if the queue is full
- Peek: Get the value of the front of the queue without removing it
Working of Queue
Queue operations work as follows:
- two pointers FRONT and REAR
- FRONT track the first element of the queue
- REAR track the last element of the queue
- initially, set value of FRONT and REAR to -1
Enqueue Operation
- check if the queue is full
- for the first element, set the value of FRONT to 0
- increase the REAR index by 1
- add the new element in the position pointed to by REAR
Dequeue Operation
- check if the queue is empty
- return the value pointed by FRONT
- increase the FRONT index by 1
- for the last element, reset the values of FRONT and REAR to -1
Queue Implementations in Python, Java, C, and C++
We usually use arrays to implement queues in Java and C/++. In the case of Python, we use lists.
# Queue implementation in Python
class Queue:
def __init__(self):
self.queue = []
# Add an element
def enqueue(self, item):
self.queue.append(item)
# Remove an element
def dequeue(self):
if len(self.queue) < 1:
return None
return self.queue.pop(0)
# Display the queue
def display(self):
print(self.queue)
def size(self):
return len(self.queue)
q = Queue()
q.enqueue(1)
q.enqueue(2)
q.enqueue(3)
q.enqueue(4)
q.enqueue(5)
q.display()
q.dequeue()
print("After removing an element")
q.display()
// Queue implementation in Java
public class Queue {
int SIZE = 5;
int items[] = new int[SIZE];
int front, rear;
Queue() {
front = -1;
rear = -1;
}
boolean isFull() {
if (front == 0 && rear == SIZE - 1) {
return true;
}
return false;
}
boolean isEmpty() {
if (front == -1)
return true;
else
return false;
}
void enQueue(int element) {
if (isFull()) {
System.out.println("Queue is full");
} else {
if (front == -1)
front = 0;
rear++;
items[rear] = element;
System.out.println("Inserted " + element);
}
}
int deQueue() {
int element;
if (isEmpty()) {
System.out.println("Queue is empty");
return (-1);
} else {
element = items[front];
if (front >= rear) {
front = -1;
rear = -1;
} /* Q has only one element, so we reset the queue after deleting it. */
else {
front++;
}
System.out.println("Deleted -> " + element);
return (element);
}
}
void display() {
/* Function to display elements of Queue */
int i;
if (isEmpty()) {
System.out.println("Empty Queue");
} else {
System.out.println("\nFront index-> " + front);
System.out.println("Items -> ");
for (i = front; i <= rear; i++)
System.out.print(items[i] + " ");
System.out.println("\nRear index-> " + rear);
}
}
public static void main(String[] args) {
Queue q = new Queue();
// deQueue is not possible on empty queue
q.deQueue();
// enQueue 5 elements
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
q.enQueue(4);
q.enQueue(5);
// 6th element can't be added to because the queue is full
q.enQueue(6);
q.display();
// deQueue removes element entered first i.e. 1
q.deQueue();
// Now we have just 4 elements
q.display();
}
}
// Queue implementation in C
#include <stdio.h>
#define SIZE 5
void enQueue(int);
void deQueue();
void display();
int items[SIZE], front = -1, rear = -1;
int main() {
//deQueue is not possible on empty queue
deQueue();
//enQueue 5 elements
enQueue(1);
enQueue(2);
enQueue(3);
enQueue(4);
enQueue(5);
// 6th element can't be added to because the queue is full
enQueue(6);
display();
//deQueue removes element entered first i.e. 1
deQueue();
//Now we have just 4 elements
display();
return 0;
}
void enQueue(int value) {
if (rear == SIZE - 1)
printf("\nQueue is Full!!");
else {
if (front == -1)
front = 0;
rear++;
items[rear] = value;
printf("\nInserted -> %d", value);
}
}
void deQueue() {
if (front == -1)
printf("\nQueue is Empty!!");
else {
printf("\nDeleted : %d", items[front]);
front++;
if (front > rear)
front = rear = -1;
}
}
// Function to print the queue
void display() {
if (rear == -1)
printf("\nQueue is Empty!!!");
else {
int i;
printf("\nQueue elements are:\n");
for (i = front; i <= rear; i++)
printf("%d ", items[i]);
}
printf("\n");
}
// Queue implementation in C++
#include <iostream>
#define SIZE 5
using namespace std;
class Queue {
private:
int items[SIZE], front, rear;
public:
Queue() {
front = -1;
rear = -1;
}
bool isFull() {
if (front == 0 && rear == SIZE - 1) {
return true;
}
return false;
}
bool isEmpty() {
if (front == -1)
return true;
else
return false;
}
void enQueue(int element) {
if (isFull()) {
cout << "Queue is full";
} else {
if (front == -1) front = 0;
rear++;
items[rear] = element;
cout << endl
<< "Inserted " << element << endl;
}
}
int deQueue() {
int element;
if (isEmpty()) {
cout << "Queue is empty" << endl;
return (-1);
} else {
element = items[front];
if (front >= rear) {
front = -1;
rear = -1;
} /* Q has only one element, so we reset the queue after deleting it. */
else {
front++;
}
cout << endl
<< "Deleted -> " << element << endl;
return (element);
}
}
void display() {
/* Function to display elements of Queue */
int i;
if (isEmpty()) {
cout << endl
<< "Empty Queue" << endl;
} else {
cout << endl
<< "Front index-> " << front;
cout << endl
<< "Items -> ";
for (i = front; i <= rear; i++)
cout << items[i] << " ";
cout << endl
<< "Rear index-> " << rear << endl;
}
}
};
int main() {
Queue q;
//deQueue is not possible on empty queue
q.deQueue();
//enQueue 5 elements
q.enQueue(1);
q.enQueue(2);
q.enQueue(3);
q.enQueue(4);
q.enQueue(5);
// 6th element can't be added to because the queue is full
q.enQueue(6);
q.display();
//deQueue removes element entered first i.e. 1
q.deQueue();
//Now we have just 4 elements
q.display();
return 0;
}
Limitations of Queue
As you can see in the image below, after a bit of enqueuing and dequeuing, the size of the queue has been reduced.
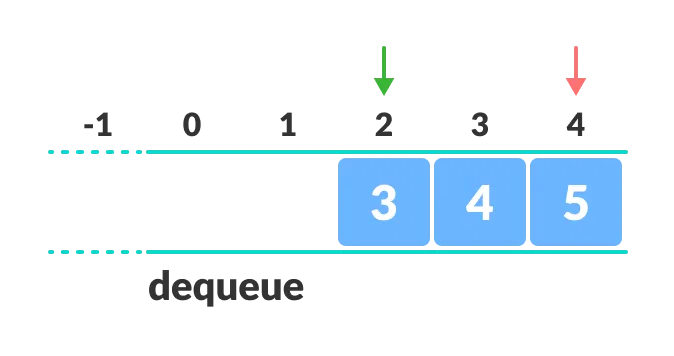
And we can only add indexes 0 and 1 only when the queue is reset (when all the elements have been dequeued).
After REAR reaches the last index, if we can store extra elements in the empty spaces (0 and 1), we can make use of the empty spaces. This is implemented by a modified queue called the circular queue.
Complexity Analysis
The complexity of enqueue and dequeue operations in a queue using an array is O(1). If you use pop(N) in python code, then the complexity might be O(n) depending on the position of the item to be popped.
Applications of Queue
- CPU scheduling, Disk Scheduling
- When data is transferred asynchronously between two processes.The queue is used for synchronization. For example: IO Buffers, pipes, file IO, etc
- Handling of interrupts in real-time systems.
- Call Center phone systems use Queues to hold people calling them in order.