Before we learn about spanning trees, we need to understand two graphs: undirected graphs and connected graphs.
An undirected graph is a graph in which the edges do not point in any direction (ie. the edges are bidirectional).
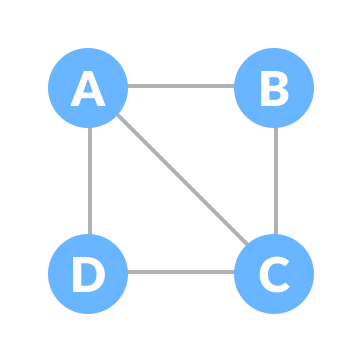
A connected graph is a graph in which there is always a path from a vertex to any other vertex.
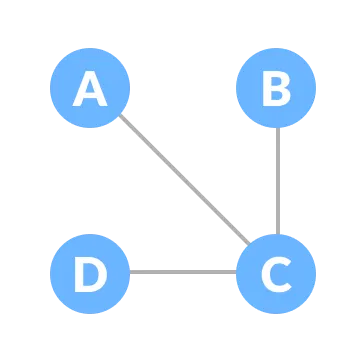
Spanning tree
A spanning tree is a sub-graph of an undirected connected graph, which includes all the vertices of the graph with a minimum possible number of edges. If a vertex is missed, then it is not a spanning tree.
The edges may or may not have weights assigned to them.
The total number of spanning trees with n vertices that can be created from a complete graph is equal to n(n-2).
If we have n = 4, the maximum number of possible spanning trees is equal to 44-2 = 16. Thus, 16 spanning trees can be formed from a complete graph with 4 vertices.
Example of a Spanning Tree
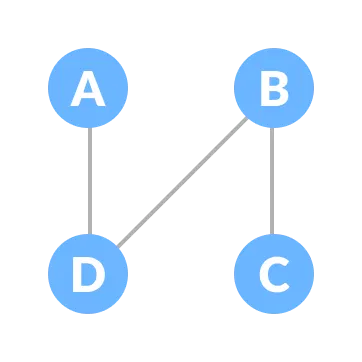
Let's understand the spanning tree with examples below:
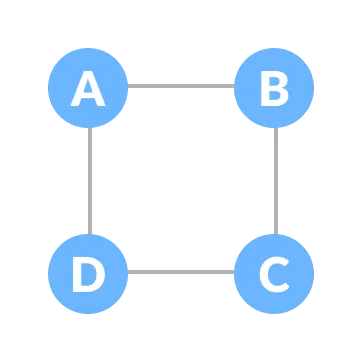
Let the original graph be:
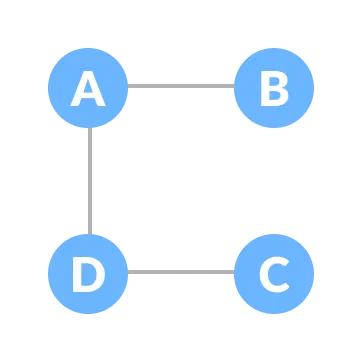
Some of the possible spanning trees that can be created from the above graph are:
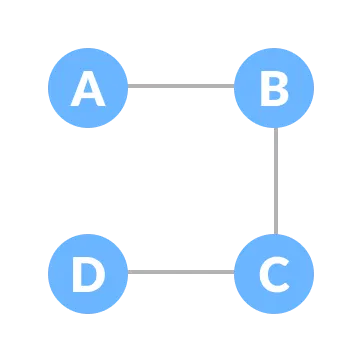
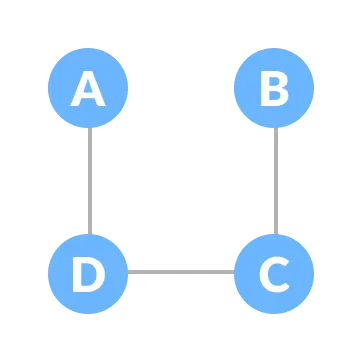
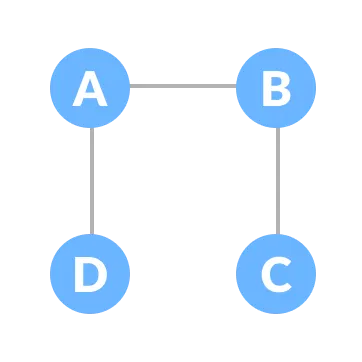
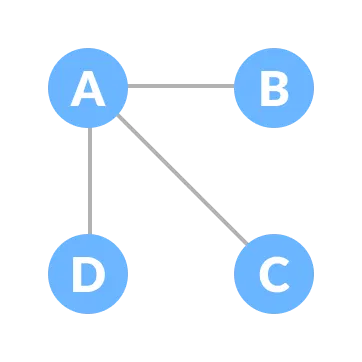
Minimum Spanning Tree
A minimum spanning tree is a spanning tree in which the sum of the weight of the edges is as minimum as possible.
Example of a Spanning Tree
Let's understand the above definition with the help of the example below.
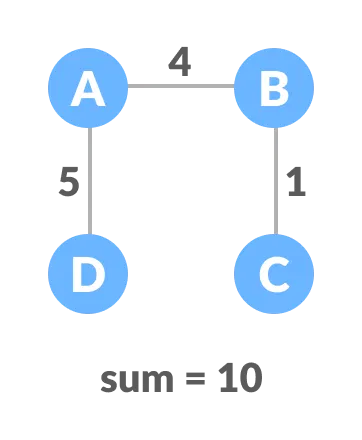
The initial graph is:
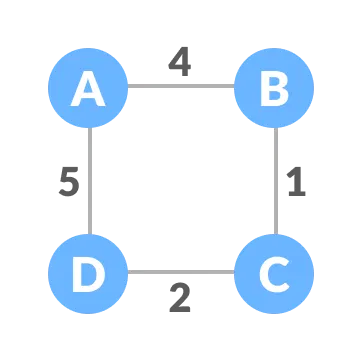
The possible spanning trees from the above graph are:
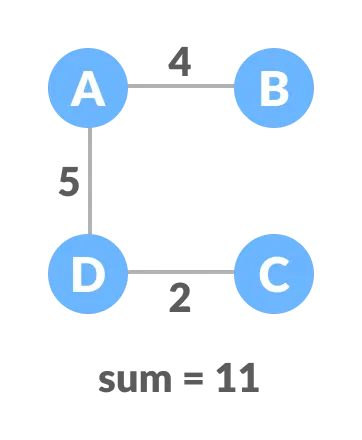
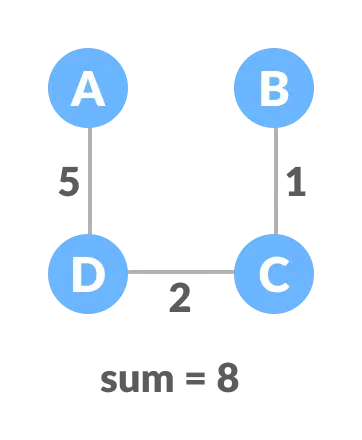
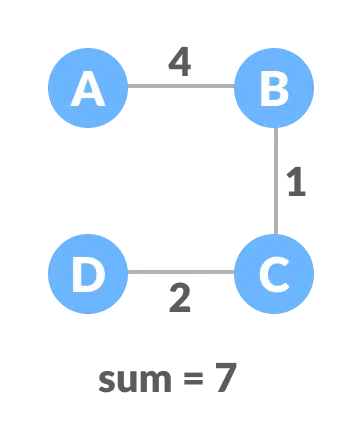
The minimum spanning tree from the above spanning trees is:
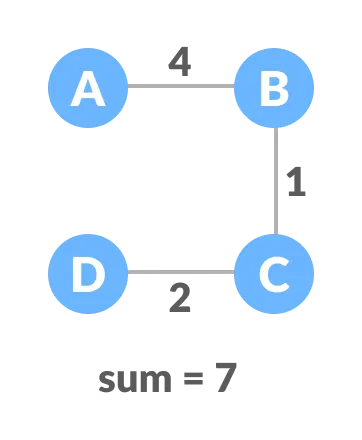
The minimum spanning tree from a graph is found using the following algorithms:
Spanning Tree Applications
- Computer Network Routing Protocol
- Cluster Analysis
- Civil Network Planning
Minimum Spanning tree Applications
- To find paths in the map
- To design networks like telecommunication networks, water supply networks, and electrical grids.